ML Functions
Activation function
Non-linear activations are what create the complex mappings between the model’s inputs and outputs. They are applied after linear transformations to introduce nonlinearity, helping neural networks learn a wide variety of phenomena.
The purpose of an activation function is to squeeze all possible values of whatever magnitude into the same range.
The activation functions can be divided in three categories
- Ridge functions
- Radial functions
- Fold functions
References: Google research
ReLU
ReLU stands for Rectified Linear Unit.
Sigmoid activation function (a.k.a. logistic function)
It is a mathematical function that maps any real number to a value between 0 and 1.
# e is the base for natural algorithm
σ(x) = 1 / (1 + e^(-x))
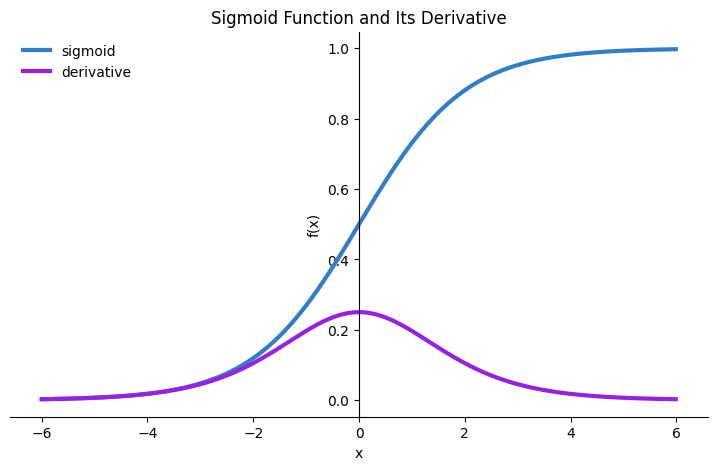
Derivative of Sigmoid function is used as the deactivation function as part of the backpropagation. It is calculated by subtracting sigmoid value from 1.
1 - σ(x)
What is the purpose of Sigmoid function in neural networks?
It is used as an activation function in neural networks. It introduces non-lienearity into the model.
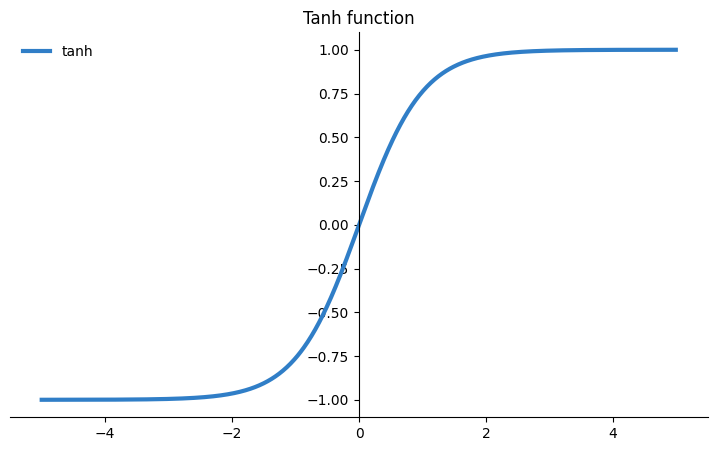
Tanh function (a.k.a. Hyperbolic tangent)
A mathematical function that maps real numbers to values between -1 and 1. It is similar to the tangent function in trigonometry, but instead of using angles, it uses real numbers as inputs.
# e is the base for natural algorithm
tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
Loss function (a.k.a. Cost function)
It is a mathematical function that quantifies the difference between the predicted output of a model and the desired or true output. It measures the model’s performance and guides the optimization process by providing feedback on how well the model fits the data.
Mean squared error (MSE): This is the average of the squared differences between the predicted and true values.
Root mean squared error (RMSE): This is the square root of the MSE.
Mean absolute error (MAE): This is the average of the absolute differences between the predicted and true values.
L1 loss: This is the sum of the absolute differences between the predicted and true values.
L2 loss: This is the sum of the squared differences between the predicted and true values.
Cross-entropy loss: This is a measure of the divergence between two probability distributions.
Kullback-Leibler divergence (KL divergence): This is a measure of the dissimilarity between two probability distributions.
Where/How are they used?
Loss functions are essential for training machine learning models. They provide a way to measure the performance of a model and to guide the optimization process. By minimizing the loss function over the training data, we can train models that make accurate predictions on new data.
Why is it used in ML training?
The goal of training a machine learning model is to minimize the loss function over the entire training dataset. This means finding a set of model parameters that produce predictions that are as close to the true values as possible.
How is the loss function selected?
The choice of loss function depends on the task being solved and the properties of the data. For example, if the data is noisy, the MAE or L1 loss may be a better choice than the MSE, as these loss functions are less sensitive to outliers.
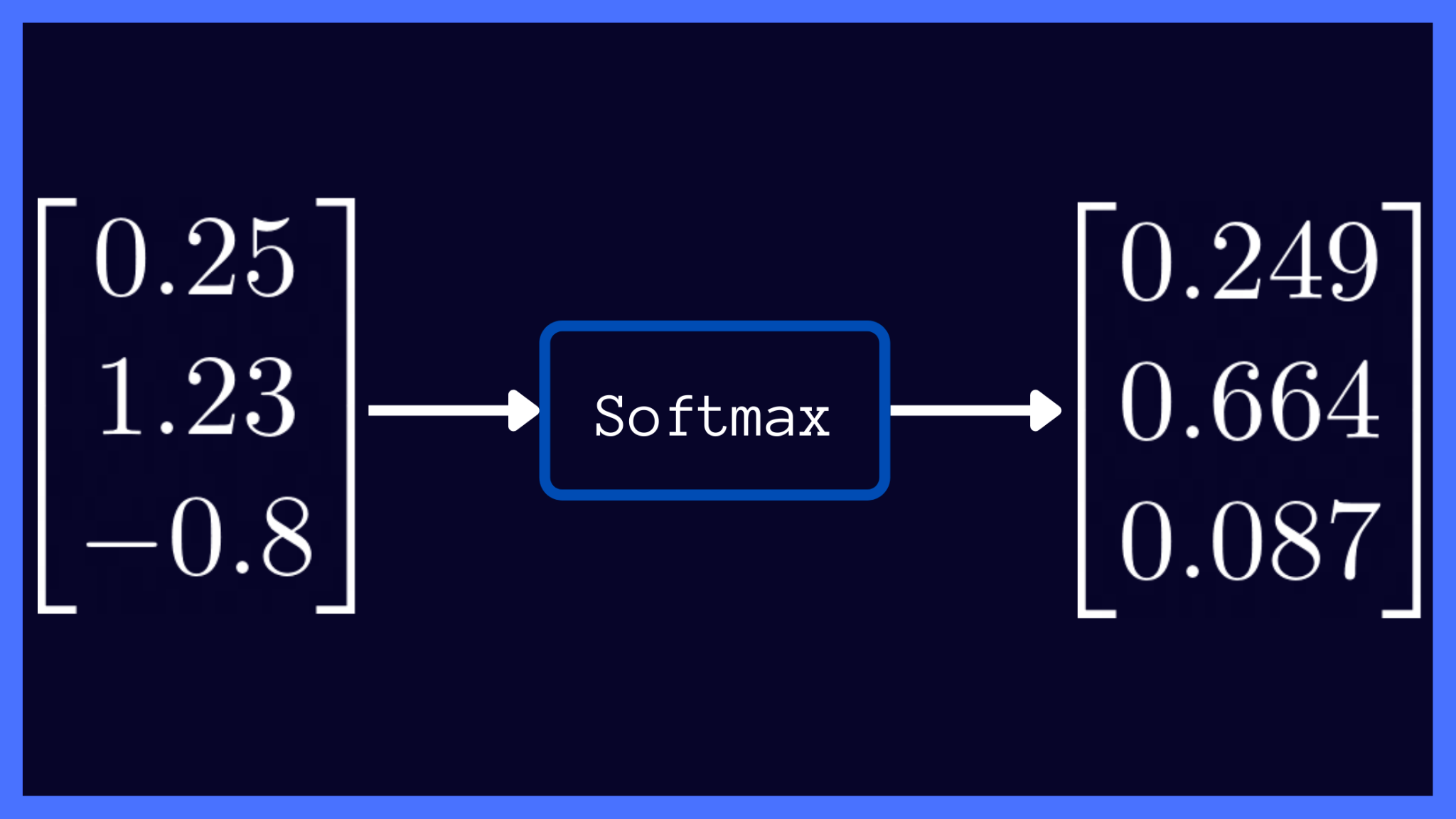
Softmax function
It is a mathematical function that transforms a vector of real numbers into a probability distribution. It is often used to normalize the neural network’s output so that the sum of all outputs is equal to 1.
It is used for multi-class classification. The output from the NN is passed to Softmax to calculate the relative probability for each of the classes.
Consider a multiclass classification problem with N classes. The softmax activation returns an output vector that is N entries long, with the entry at index i corresponding to the probability of a particular input belonging to the class i.
# z is a vector of real numbers
# exp() is the exponential function
# sum() is the sum function
softmax(z) = [exp(z[i]) / sum(exp(z))]
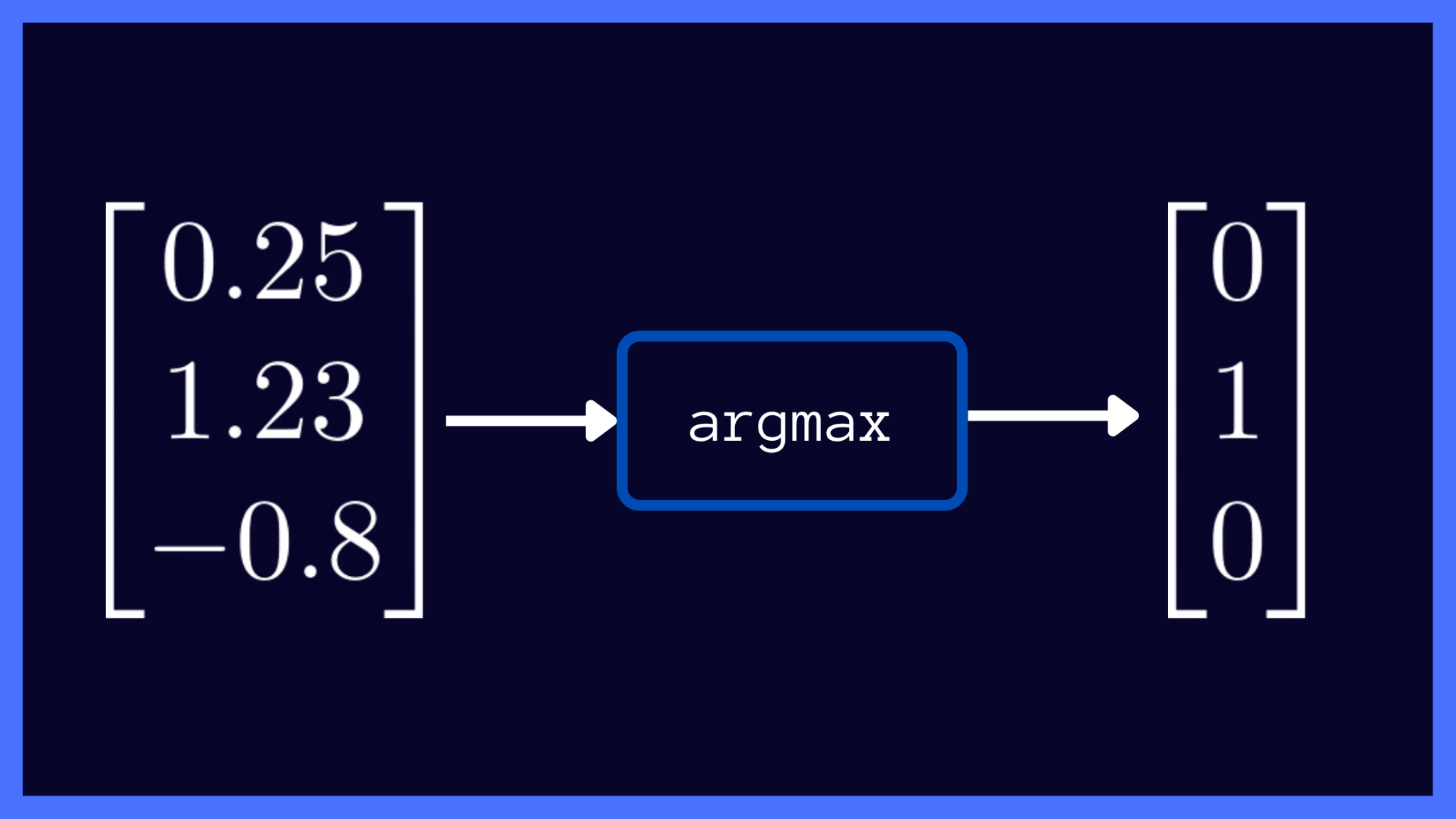
Argmax function
Also known as the Argument of the maximum, is a mathematical function tha finds the index of the element in a given array or list that has the maximum value.
argmax(x) = i such that x[i] ≥ x[j] for all j
The argmax function in the code above returns the index i of the element in the array x that has the greatest value compared to all other elements x[j].
Logits
An overloaded term that has different meaning based on the context.
In Machine Learning - Neural Network context, It refers to the raw output predictions from the model.
In effect logit referes to vector of raw (non-normalized) predictions that are generated by the model.
This is the tensor on which you apply the:
- Softmax function to get the probabilities for the predicted class
E.g., DNA model may indicate a person as:
10% European 70% Persian 20% Indigenous
- Argmax function to get the predicted class
e.g., a language prediction model may predict the language
Hindi 0 German 1 Russian 0 French 0
The size of the logits vector depends on the dimension of the output layer of the model. A classification model that is built for prediction across 10 classes will have a logit vector size = 10.